Lógica Matemática

 Lógica Matemática

La lógica es disciplina a dedicada a identificar los principios generales , formas y estructuras o esquema de razonamiento formales, con el fin de determinar si un argumento es o no válido.

Definición

-La lógica tiene un lenguaje exacto.
-Es necesario redactar un conjunto de reglas que sean perfectamente claras y definidas
- La lógica nos ayudará a aprender una forma de razonar que es exacta y a la vez muy útil

Proposiciones 

Una proposición es todo enunciado respecto al cual se disponga de un criterio que permita afirmar inequívocamente que su contenido es verdadero falso .Tiene sentido completo y valor de verdad

Ejemplos. 

Determine cuales de las siguientes oraciones son proposiciones

a. 13 es un número par (V)
b. Leonel Fernández fue presidente de República Dominicana (V)
c. ¿Qué hora es? (F)
d. x+3=5 (F)

Criterio

La verdad o falsedad de algunas oraciones es relativa, es decir, dependen del contexto y el momento determinado en que se hagan las afirmaciones, del criterio utilizado para calificarlas o de las personas que hagan las calificaciones.

Principios lógicos 

1) Tercero excluido Cada proposición es o verdadera o falsa. Es decir, no existe una tercera posibilidad. 

2) No contradicción Ninguna proposición es, a la vez, verdadera y falsa. 

Dar a entender

Las proposiciones se representarán con letras minúsculas, generalmente p, q, r, s, t, etc. Cuando convenga se usará una letra acompañada de un subíndice, por ejemplo p1, p2, p3, etc. 

▪ Valor de verdad

En el caso de la lógica bivalente, que es la que se trata en este texto, los valores de verdad son verdadero y falso que usualmente se denotan con las Proposiciones letras V y F respectivamente.

Clasificación

Simples o Atómicas: Tiene valor de verdad cuando se puede asegurar que

es V o F

Compuestas o moleculares: Mas de una proposición simples, unidas con un conector lógico

Proposiciones simples: Ejemplos

p: La tierra es plana

q: El perro ladra todo el día

r: La pared es azul

▪ Proposiciones compuestas: Ejemplos

p: El número 2 es par y el número 5 es impar

q: Charlies Darwin fue un biólogo y descubrió las Islas Galápagos

r: Machala es una ciudad y es muy hermosa

Negación

La negación es un conectivo lógico unitario que se aplica a una sola proposición, dando como resultado una proposición compuesta cuyo valor de verdad es opuesto al de la proposición original. 

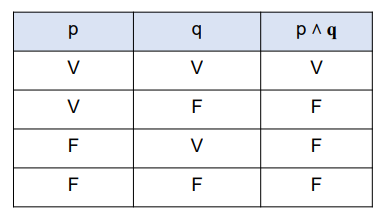
▪ Tabla de verdad

La conjunción es verdadera solo cuando ambas proposiciones componentes son verdaderas, y resulta falsa en los demás caso

Disyunción inclusiva

La disyunción inclusiva es un conectivo que aplicado a dos proposiciones p y q, genera como resultado la proposición compuesta cuyo valor de verdad es falso cuando ambas componente sean falsas y verdadero cuando al menos una de las

componentes sea verdadera

Tabla de verdad

La proposición inclusiva resulta falsa cuando todas las proposiciones componentes son falsa, y verdadera cuando al menos una de ellas es verdadera.

Disyunción exclusiva

La disyunción exclusiva es un conectivo que aplicado a dos proposiciones cualesquiera p y q da como resultado una proposición compuesta que será verdadera si sólo una de las proposiciones que la componen es verdadera.

Tabla de verdad

La disyunción exclusiva resulta verdadera solo cuando una de las dos proposiciones componentes es verdadera, y falsa en los demás caso.